A data structure is the organization of data in a way so that it can be used “efficiently“

In order to use data efficiently, we have to store it efficiently.

Efficiency of data structure is always measured in terms of TIME and SPACE.

An ideal data structure could be the one that takes least possible time for all its operations and consumes the least memory space.

Our focus will be on finding the “TIME COPLEXITY”.

On what basis, we could compare the time complexity of the data structure?

On the basis of operations performed on them

How to find the time complexity or running time of an operation performed on data structure?

Examining the exact running time is not the best solution to calculate the “Time Complexity”

Measuring the actual running time is not practical at all.

The running time generally depends on the size of the input.

Example

If an array has 3 elements: 4,1,2 and an element 3 needs to add at the start of an array, it has to shift 3 elements to right, if 1 shift takes 1 unit of time then it takes total 3 units of time.

If there are 10,000 shifts there will 10,000 units of time.

Therefore if the size of the input is then f(n) is a function of n denotes the time complexity.

In other words, f(n) represents the number of instructions executed for the input value n.

Asymptotic analysis of an algorithm refers to defining the mathematical foundation/framing of its run-time performance. Using asymptotic analysis, we can very well conclude the best case, average case, and worst case scenario of an algorithm.

Asymptotic analysis is input bound i.e., if there’s no input to the algorithm, it is concluded to work in a constant time. Other than the “input” all other factors are considered constant.

Asymptotic analysis refers to computing the running time of any operation in mathematical units of computation.

Using asymptotic analysis, we can get an idea about the performance of the algorithm based on the input size. We should not calculate the exact running time, but we should find the relation between the running time and the input size. We should follow the running time when the size of input is increased.

For the space complexity, our goal is to get the relation or function that how much space in the main memory is occupied to complete the algorithm.

For example, the running time of one operation is computed as f(n) and may be for another operation it is computed as g(n²). This means the first operation running time will increase linearly with the increase in n and the running time of the second operation will increase exponentially when n increases. Similarly, the running time of both operations will be nearly the same if n is significantly small.

Usually, the time required by an algorithm falls under three types −

• Best Case − Here the lower bound of running time is calculated. It describes the behavior of algorithm under optimal conditions.
• Average Case − In this case we calculate the region between upper and lower bound of the running time of algorithms. In this case the number of executed operations are not minimum and not maximum.
• Worst Case − In this case we calculate the upper bound of the running time of algorithms. In this case maximum number of operations are executed.

Asymptotic Notations

Following are the commonly used asymptotic notations to calculate the running time complexity of an algorithm.

• Ο − Big Oh Notation
• Ω − Big Omega Notation
• Θ − Theta Notation
• o − Little Oh Notation
• ω − Little Omega Notation

Big O Notation

The notation Ο(n) is the formal way to express the upper bound of an algorithm’s running time. It measures the worst case time complexity or the longest amount of time an algorithm can possibly take to complete.

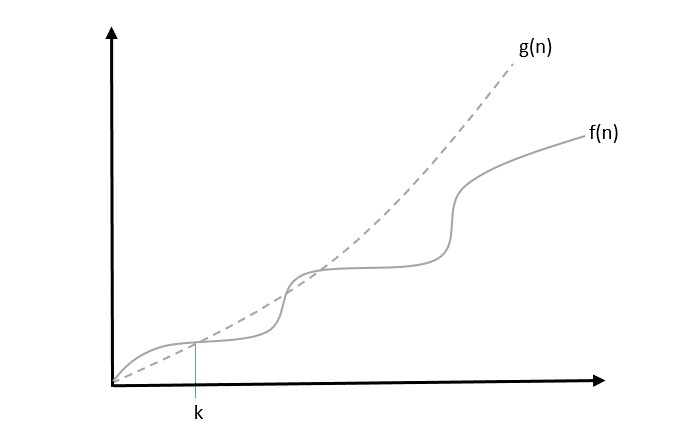
For example, for a function f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n0 such that g(n) ≤ c.f(n) for all n > n0. }

Example

Let us consider a given function, f(n) = 4.n³+10.n²+5.n+1.

Considering g(n) = n³

    f(n) ≥ 5.g(n) for all the values of n > 2.

Hence, the complexity of f(n) can be represented as O (g (n) ) ,i.e. O (n³).

Theta Notation, θ

The notation θ(n) is the formal way to express both the lower bound and the upper bound of an algorithm’s running time. Some may confuse the theta notation as the average case time complexity; while big theta notation could be almost accurately used to describe the average case, other notations could be used as well. It is represented as follows −

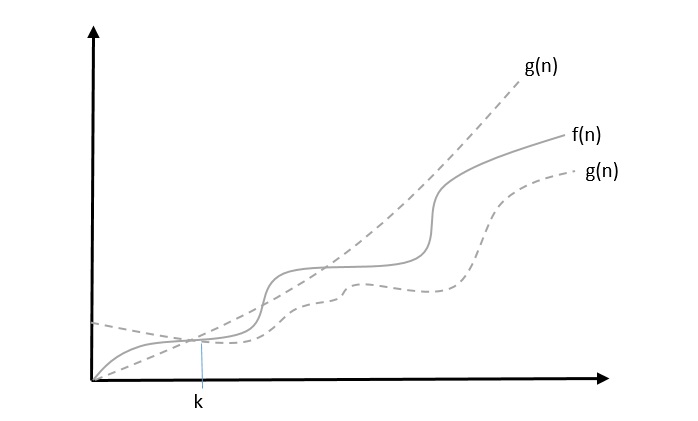
θ(f(n)) = { g(n) if and only if g(n) = Ο(f(n)) and g(n) = Ω(f(n)) for all n > n0. }

Example

Let us consider a given function, f(n) = 4.n³+10.n²+5.n+1

Considering g(n) = n³ , 4.g(n)≤ f(n)≤ 5.g(n) for all the values of n.

Hence, the complexity of f(n) can be represented as Ɵ (g (n) ) ,i.e. Ɵ (n³).

Little Oh (o) and Little Omega (ω) Notations

The Little Oh and Little Omega notations also represent the best and worst case complexities but they are not asymptotically tight in contrast to the Big Oh and Big Omega Notations. Therefore, the most commonly used notations to represent time complexities are Big Oh and Big Omega Notations only.

Common Asymptotic Notations

Following is a list of some common asymptotic notations −

constant	O(1)
logarithmic	O(log n)
linear	O(n)
n log n	O(n log n)
quadratic	O(n2)
cubic	O(n3)
polynomial	nO(1)
exponential	2O(n)

Examples

Examples:

Linear Time Complexity. O(n)

int n;
cin>>n;
int a = 0;
for (int i=1; i<=n; i++)
{
    a = a+1;
}

Quadratic time Complexity. O(n²)

int n;
cin>>n;
int a=0;
for (int i=1; i<=n; n++)
{
    for(int j=1; j<=n; j++)
    {
       a = a+1;
    }
}

Time Complexity: O(n+m)

int n,m;
cin>>n>>m;
int a=0;
for(int i=1; i<=n;i++)
{
    a = a+1;
}
for (int j=1; j<=m; j++)
{
   a = a+1;
}

Time complexity: O(n*m)

int n,m;
cin>>n>>m;
int a=0;
for (int i=1; i<=n; i++)
{
  for(int j=1; j<=m; j++)
   {
     a = a + rand();
   }
}

Time complexity: O(log(n))

int n;
cin>>n;
int a=0; i=n;
while(i>=1)
{
   a = a+ 1;
   i/=2;
}