Divide and Conquer

The divide and conquer approach requires recursively breaking a problem into smaller subproblems (the divide part) until they become easy enough to be solved directly.

The merge sort algorithm is the canonical example given for the Divide and Conquer design paradigm. In merge sort, for example we keep dividing the array into two parts until the size of the array is 1 and we know how we can sort an array with just one element (It’s already sorted). The next step is to somehow combine the solutions of the smaller subproblems to obtain the solution of the original problem (the conquer part). This step is usually tricky.

In merge sort we used the ”merge” algorithm to sort the larger array from two sorted halves.
Next, we will discuss two more Divide and Conquer algorithms. The first is the problem of counting
inversions, as follows. The second is the problem of finding closest pair of points among a set of points in
2-dimensional Euclidean space. We present the brute-force approach to solve this problem and improve it using the divide and conquer approach.

Counting Inversions

Problem : Given an array A an inversion is defined as a pair i, j such that i < j ∧ A[i] > A[j]. We want to find how many such pairs are in A.

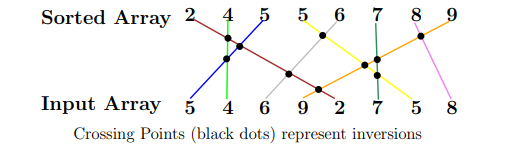
Example : Let A = 5 4 6 9 2 7 5 8

Then the inversions for this array are
{(1, 2),(1, 5),(2, 5),(3, 5),(3, 7),(4, 5),(4, 6),(4, 7),(4, 8),(6, 7)}
Solution : One way to solve is problem is to simply check all pairs i, j and see how many of them are
inversions. There are (n2) pairs so that would take about n²/2 steps.

That algorithm would work as follows
Algorithm 1 : Counting Inversions Using Brute Force
count ← 0
for i = 1 to n do
for j = i+1 to n do
if A[i] > A[j] then
count ← count + 1

As computer scientists, however, we always want to come with better, more efficient algorithms. But why
should we think that a better solution should exist for this problem?

Well one reason is that this problem is somewhat related to sorting an array (Infact the number of inversions is used as a measure for the sorted-ness of an array). When we’re sorting an array we’re basically removing all the inversions. And we know we can sort an array in n log(n) steps. The algorithm for that was discussed in the last class. So it makes sense that there should be a similar algorithm that can count inversions in about the same time too. We used the divide and conquer approach to obtain a better running time for sorting. So let’s try to do something similar for counting inversions too.

How should be break this problem?
If we divide an array into two halves, then we can split the inversions into 3 types:

• Left-Left inversions
• Right-Right inversions and
• Left-Right inversions.

For example, consider the following array A:

We’ll refer to the left and right halves of the array as L and R.

Then Left-Left inversions are those which only involve pairs from L.

Similarly the Right-Right inversions are the inversions that involve pairs from only R.

Left-Right inversions are pairs that involve one element from L and one element from R.

The Left-Left and Right-Right inversions will be found by recursively dividing the array into even smaller parts.

The problem is finding the Left-Right inversions. If we can find the Left-Right inversions in n steps then we can solve the problem in n log(n) steps.

The algorithm would have the same recurrence relation as the merge sort algorithm and hence the same running time.
The problem of finding the left-right inversions is equivalent to finding the ranks in R of all the elements of L.

We know that if the two arrays R and L are sorted then we can find the ranks in n steps.

So while counting the inversions in the left and right halves of the array we’ll do some extra work and also sort them.

The idea is that even though we do the some extra work in sorting, the overall time will be reduced because now we can find the inversions much faster.

Let’s see how that algorithm would work.

Algorithm 2 : Counting Inversions using Divide and Conquer

function CountInversions (A)
if Size(A) == 1 then return (A, 0)
L ← A[1, 2, . . . , n/2]
R ← A[n + 1, n + 2, . . . , n]
(sortedL, invl,l) ← CountInversions(L)
(sortedR, invr,r) ← CountInversions(R)
invl,r ← sum(FindRanks(L, R)) . takes n steps
return (Merge(L, R), invl,l + invr,r + invl,r) . merge takes n steps

Collaborative Filtering

One of the areas in which the problem of counting inversions comes up is in Recommender Systems.

A recommender system tries to predict the ’rating’ a user gives to a particular item.

Like how YouTube tries to recommend you videos based on your viewing history, or how IMDb recommends movies.

One technique used in recommender systems is that of Collaborative Filtering.

”Collaborative filtering is a method of making automatic predictions (filtering) about the interests of a user by collecting preferences or taste information from many users (collaborating).

The underlying assumption of the collaborative filtering approach is that if a person
A has the same opinion as a person B on an issue, A is more likely to have B’s opinion on a different issue x than to have the opinion on x of a person chosen randomly” (Wikipedia).
The way this is done is as follows.

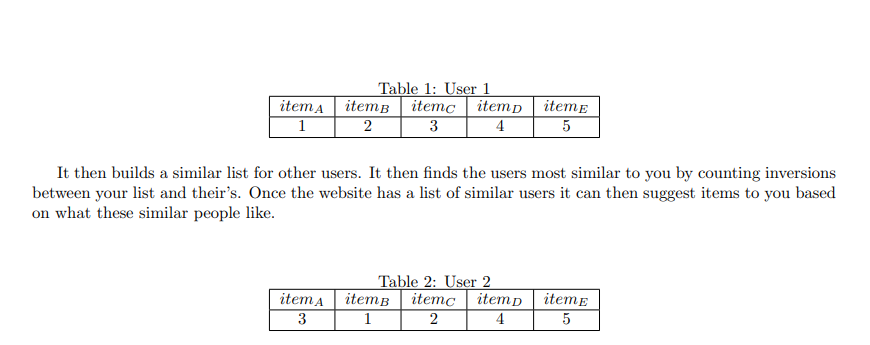
Based on your activity on the website(How many times you view a particular item, the review you’ve given some item etc) the website builds a list containing your relative preference to various items.